Samenvatting Fysica 6de middelbaar Examen juni
Dit is een samenvatting van Fysica voor het examen van juni voor het 6de middelbaar. Het is gebaseerd op het boek Fysica vandaag voor de 1 uurs wetenschappen.
Belangrijke definities of begrippen zullen in dit kader gegeven worden
Disclaimer: dit is slechts een samenvatting. Ik probeer deze zo volledig mogelijk te maken maar ik raad toch aan om je notities nog eens te bekijken!
Weglatingen: bewijs arbeid-energie theorema en bewegingsvergelijking van een harmonische trilling (1.2 in boek)
0. De eenparige cirkelbeweging
De hoeksnelheid is de verhouding tussen de verandering van de middelspunthoek over een bepaald tijdsinterval.
Dus:
$$ \omega = \frac{\Delta \theta}{\Delta t} = constant \ \text{Waarbij $\theta$ de grootte van de middelpuntshoek is} $$
De hoeksnelheid beschouwen we als constant omdat het hier gaat over een eenparig cirkelbeweging (ECB). Deze grootheid wordt uitgedrukt in rad/s.
We kunnen ook naar de periode zoeken hoe lang het duurt om één cirkelomtrek (een middelpuntshoek van 360 ° of in radialen 2 pi rad) te doorlopen, deze tijd noemen we de periode van de ECB.
We vertrekken van de hoeksnelheid, we willen nu vinden hoe lang het voorwerp erover doet om een middelpuntshoek van 360° te voltooien:
$$ \omega = \frac{2\pi}{T} $$
De periode T is dan te vinden door te formule om te vormen naar T.
We kunnen ook de frequentie van de ECB bekijken. De frequentie is het aantal keer per tijdseenheid dat het voorwerp de beweging voltooid.
Vb. Stel het duurt 3 seconden voordat een voorwerp een ECB voltooid. Logisch vloeit hieruit dat per seconden de de beweging voor 1/3 wordt uitgevoerd.
De frequentie is dus 1/3 Hz, algemeen:
$$ f = \frac{1}{T} $$
Maar wat weten we over de positie van het voorwerp in de cirkel? We kunnen haar x-cooördinaat vinden door gebruik te maken van cosinus en sinus.
Zoals te zien is op deze figuur van een cirkel:
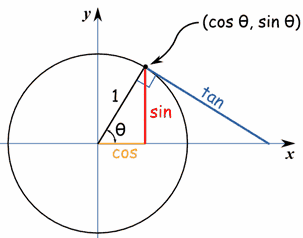
r is telkens de straal van de cirkel
$$ x = r \cdot \cos \theta $$
$$ y = r \cdot \sin \theta $$
Als de hoeksnelheid bekend is kunnen we via de formule van de hoeksnelheid ook de middelpuntshoek veranderen in de bovenstaande formule:
$$ \omega = \frac{\theta}{t} $$
Dus:
$$ \omega \cdot t = \theta $$
Ingevuld:
$$ x = r \cdot \cos(\omega \cdot t) $$ $$ y = r \cdot \sin(\omega \cdot t) $$
Net zoals bij de eenparige rechtlijnige beweging (ERB) en de EVRB kunnen we dit gaan afleiden om de snelheid en de versnelling te bekomen.
Voor de snelheid krijgen we dan:
$$ v = r \cdot \omega $$ of als we de hoeksnelheid vervangen door haar defenitie $$ v = r \frac{2\pi}{T} $$
Voor de versnelling krijgen we dan:
$$ a = r \cdot \omega^2 $$
0.1 De dynamica van de eenparige cirkelbeweging
Een voorwerp dat een eenparige cirkelvormige beweging uitvoert moet op één of andere manier telkens aangetrokken zijn tot het middelpunt van de cirkel. Anders kan het voorwerp natuurlijk geen cirkelvormige beweging uitvoeren.
Een voorbeeld daarvan is kogelslingeren, het voorwerp doet eerst een cirkelvormige beweging maar vanaf dat de atleet de bal loslaat gaat hij vliegen in een rechtlijnige beweging.
De kracht die het voorwerp naar het midden aantrekt noemen we de middelpuntszoekende kracht.
Vanuit de tweede wet van Newton ( F = m * a) die kracht in verband stelt met massa en versnelling kunnen we voor de eenparige cirkelvormige beweging de volgende vergelijking opstellen:
We hebben in het vorige deel berekend wat de versnelling van een ECB moet zijn, dit was gelijk aan: $$ a = r \cdot \omega^2 $$ Nu kunnen we deze “a” invullen in de vergelijking van de tweede wet van Newton: $$ F = m \cdot r \cdot \omega^2 $$ of in functie van de snelheid v $$ F = m \cdot \frac{v^2}{r} = \frac{m \cdot v^2} {r} $$
Dit is dus de middelpunt zoekende kracht of de epicentrische kracht.
1. Mechanica: dynamica
1.5. Enkele bijzondere krachten
1.5.1 De universele gravitatiekracht
De grativitatiekracht is een kracht die optreedt tussen twee puntmassa’s die een afstand r van elkaar verwijderd zijn. Deze kracht is rechtevenredig met het product van deze puntmassa’s en omgekeerd evenredig met het kwadraat van de afstand tussen deze twee puntmassa’s.
Deze gravitatiekracht is er bijvoorbeeld bij planeten die rond de zon draaien.
De algemene formule wordt dan:
$$ F = G \cdot \frac{m_1 \cdot m_2}{r^2} $$
Dus hoe groter de afstand tussen beide puntmassa’s hoe kleiner de gravitatiekracht. Hoe kleiner de afstand des te groter de kracht zal worden.
Een zwaardere massa (bv. een grotere ster) zal een grotere gravitatiekracht kunnen uitoefenen op het andere hemellichaam.
De G of gravitatieconstante is een constant getal vooraf bepaald. Dat is gelijk aan:
$$ G = 6,67 \cdot 10^{⁻11} $$
1.5.2 Gravitatiekracht als middelpuntzoekende kracht
We kennen het allemaal wel: satelieten of ruimtestations die in een cirkelvormige baan bewegen rond de aarde.
Opdat de sateliet een ECB beweging zou uitvoeren is er een middelpuntszoekende kracht nodig, en deze is (zie ook 0.1):
We kunnen deze formule op een planeet toepassen met straal r en waarrond een ruimtetuig op hoogte h vliegt.
$$ F_{MZ} = \frac{m \cdot v^2}{r + h} \text{(1)} $$
De cirkelvormige beweging heeft een middelpuntzoekende kracht. In dit geval wordt deze geleverd door de gravitatiekracht.
Als we dit verder uitwerken naar de snelheid van de baan van het ruimtetuig:
$$ v = \sqrt{G \cdot \frac{m_{planeet}}{r + h}} $$
Hieruit kunnen we concluderen dat het niet uitmaakt wat de massa is van het ruimtetuig, haar snelheid rond de planeet zal altijd hetzelfde blijven.
1.5.3 De zwaartekracht
De zwaartekracht als bijzonder geval van de gravitatiekracht
De formule voor gravitatiekracht is gelijk aan:
$$ F_{z} = m \cdot g $$
waarbij g = 9,81 m/s^2
Maar we kunnen deze formule ook bekomen door gebruik te maken van de universele gravitatiekracht:
$$ F_G = G \cdot \frac{m_{aarde} \cdot m}{r^2} $$
Gezien we de straal en massa van de aarde kennen en deze (ongeveer) constant zijn kunnen we bepaalde delen van de vergelijking schrappen (a is een constant getal).
$$ F_G = a \cdot m $$
a zal dan gelijk zijn aan:
$$ a = \frac{m_{aarde}}{r^2} $$
We hebben bijna onze oorspronkelijke vergelijking. We moeten alleen de constante “a” nog in “g” veranderen.
Formule: $$ F_z = m \cdot g $$
Gewicht van een lichaam
Een gewicht zeker niet te verwarren met de massa, is de grootte van de kracht die een voorwerp uitoefent op zijn steun.
Dus als een persoon ergens stil neer zit dan is zijn gewicht gelijk aan de zwaarte kracht die op hem inwerkt. (zijnde F = m * g, met g = 9,81) Het is dus niet correct te zeggen dat je zoveel kg weegt, kg gebruikt men voor de massa. Een weegschaal kan bij bepaalde omstandigheden zelfs een andere massa aangeven dan in realiteit is.
Een voorbeeld:
Een visser heeft een vis aan een veer met veerbalans gehangen, die een bepaald gewicht aangeeft. Deze visser is niet echt normaal want hij staat met zijn vis in een lift!
Wanner de lift plots naar beneden gaat ziet de visser dat de veerbalans een kleiner gewicht aangeeft dan in het begin.
Hoe komt dit?
Wel er werken bepaalde krachten op de veer in, namelijk de veerkracht zelf (F_v) en de zwaartekracht (F_z).
Vanuit het tweede beginsel van Newton weten we dat deze kracht gelijk moet zijn aan de massa vermenigvuldigd met de versnelling:
$$ F_z - F_v = m \cdot a \text{ (Veerkracht is negatief want wijst in tegenstelde zin van de zwaartekracht)} $$
Uitgewerkt:
$$ m \cdot g - F_v = m \cdot a $$
Maar we willen weten wat de veerbalans zal worden dus wat de grootte van F_v is.
$$ F_v = - m \cdot a + m \cdot g = m ( g - a ) $$
Hieruit kunnen we concluderen dat hoe grote de versnelling naar beneden hoe kleiner het gewicht dat de veerbalans aangeeft zal worden.
Omgekeerd kan dit ook, wat als de lift zou stijgen? Wel dan zal er eenzelfde versnelling omtreden maar met tegengestelde zin:
$$ F_v = m ( g - (-a)) = m ( g + a ) $$
2. Arbeid
2.1 Arbeid geleverd door een constante kracht
Arbeid is het werk dat een bepaalde kracht levert eventueel over een bepaalde afstand
2.1.1 Kracht en verplaatsing hebben dezelfde richting
Een kracht zal een bepaalde grootte arbeid leveren afhankelijk van de afstand waarover hij gaat. Het verband is recht evenredig dus:
Symbool W staat voor arbeid, de eenheid is joule of J
$$ W = F \cdot \Delta x $$
Dus een kracht van 1 N levert 1 J arbeid als het over 1m verplaats wordt.
2.1.2 Kracht en verplaatsing hebben een verschillende richting
Als de kracht en de verplaatsing niet dezelfde richting hebben moeten we onze formule lichtjes aanpassen.
We verwerken er een cosinus in zodat de vector van de kracht kan geprojecteerd worden op de x-as of de verplaatsingsvector.

De formule wordt dan:
$$ W = F \cdot \cos(\alpha) \Delta x $$
2.3 Arbeid geleverd door een niet-constante (variable) kracht
Stel dat de kracht over een bepaalde afstand niet altijd constant is. Stel dat een persoon bij 1m minder kracht levert dan bij 2m (bijvoorbeeld bij het starten van een loopwebstrijd start je vanuit rust tot een bepaalde snelheid).
We kunnen dan de relatie tussen de afstand en de kracht uitdrukken op een grafiek.
We zetten op de x-as de afstand (x) en op de y-as de geleverde kracht. Om dan de totale arbeid binnen een bepaalde interval op de grafiek te vinden moeten binnen dat interval alle waarden van de kracht vermenigvuldigen met alle waarden van de afstand.
We zouden dit kunnen doen door het interval in deelintervallen in te delen en dan van elk deelinterval de afstand en de geleverde kracht te nemen en deze dan met elkaar te vermenigvuldigen. Maar dit is niet echt nauwkeurig, we zouden de deelintervallen dus zeer klein moeten maken. Met andere woorden we gaan de oppervlakte zoeken tussen de curve en de x-as in een bepaald interval, met andere worden we moeten de intergraal berekenen van die grafiek.
Om deze integraal uit te werken hebben we natuurlijk de krachtfunctie nodig die op dat moment inwerkt op een voorwerp.
2.4 Vermogen
Het is leuk om te weten wat de arbeid van iets is, maar soms is het ook handig om te weten hoe snel iemand de gegeven arbeid kan uitvoeren. De tijd waarin een arbeid wordt uitgevoerd noemen we het vermogen.
Het vermogen wordt dus:
Formule vermogen $$ P = \frac{W}{t} $$
2.5 Potentiële energie
2.5.1 Elastische potentiële energie
Is de energie dit nodig is bij kracht dat een veer met een bepaalde veerconstante k over een bepaalde uitrekking (x) uitoefent.
Formule: $$ E_k = \frac{1}{2} k \cdot x^2 $$
2.5.2 Gravitationele potentiële energie
Een voorwerp dat naar omlaag valt door de zwaartekracht F_z heeft als arbeid (zie 2.1.1: kracht en verplaatsing hebben dezelfde richting):
$$ W = F \cdot x $$
We kunnen x vervangen door een y omdat het naar beneden valt (naar analogie met de y-as is een assenstelsel) We kunnen ook de F van de zwaartekracht vervangen omdat we die al kennen:
$$ W = m \cdot a \cdot y $$
Dus de potentiële gravitatie energie is:
$$
E_p = m \cdot g \cdot y $$
2.6 Beginsel van behoud van mechanische energie
Het beginsel van behoud van energie zegt dat als er een verandering in een type energie zich bevind dat het in het andere ook moet voorkomen. Bijvoorbeeld: als de kinetische energie veranderd moet ook de potentiële energie veranderen.
Met andere woorden de kinetische energie opgeteld met de potentiële energie moet steeds constant zijn. Kinetische energie:
$$ E_k = \frac{m \cdot v^2}{2} \text{ (zie arbeidsenergie-theorema in het boek)} $$
Een ander voorbeeld: een glijbaan.
Als een kind van de glijbaan glijdt zal het eerst de zwaartekracht ondervinden wanneer vervolgens het kind beneden is zal het een bepaalde snelheid moeten hebben (zie kinetische energie) om de verandering in de zwaartekracht te kunnen verantwoorden.
Met getallen:
Hoogte glijbaan: 6,50m Massa kind: 11,2 kg
Vraag: hoe groot is de snelheid van het kind beneden
Oplossing (A is de beginpositie boven, en B is de eindpositie beneden)
$$ E_pA + E_kA = E_pB + E_kB $$
Hier staat dat de energie vanboven op de glijbaan gelijk moet zijn als onder de glijbaan. We gebruiken hier ook de potentiële energie van de zwaartekracht omdat de zwaartekracht (E_p) vanboven op de glijbaan inwerkt.
Uitgewerkt wordt dat dan: $$ m \cdot g \y + \frac{m \cdot v^2}{2} = m \cdot g \y + \frac{m \cdot v^2}{2} $$
Met getallen:
$$ 11,2 kg \cdot 9,81 \cdot 6,5m + \frac{11,2 kg \cdot 0 m/s}{2} = 11,2 kg \cdot 9,81 \cdot 0m + \frac{11,2 kg \cdot v^2}{2} $$
Nu hebben we nog maar één onbekende “v”, en dat is nu net wat we zoeken. We kunnen dit uitrekenen en dan bekomen we de v beneden aan de glijbaan. V wordt hier dan: 11,3 m/s.
3. Periodieke verschijnselen
3.1 De vrij ongedempte harmonische trilling
3.1.1 Enkele begrippen
Een trilling is een periodieke beweging van een voorwerp. De beweging bestaat uit een reeks van opeenvolgende bewegingen die identiek zijn, zo één beweging noemne we een cyclus.
De tijd dat een voorwerp doet over zo’n cyclus noemen we de periode. Hoeveel keer per tijdseenheid dat het voorwerp een cyclus uitvoert noemen we de frequentie.
3.1.2 Kenmerkende grootheden
Een trilling is harmonisch als het aan de volgende vergelijking voldoet:
$$ y = A \cdot \sin(\omega t + \phi) $$
Vanuit de wiskunde en de sinus functie kunnen we het volgende uit de vergelijking halen:
- De amplitude (A) is de maximale uitwijking die de trilling kan hebben, deze kan -A of A worden, de sinus is immers cyclis en heeft ligt altijd tussen -1 en 1.
- De phi is noemt men de beginfase, het is namelijk het enige wat overblijft binnen de sinus functie bij t = 0. Dus het is de positie die het voorwerp inneemt op tijdstip 0.
- De omega is kan gebruikt worden om de periode te bepalen.
Even terug uit de opsomming. Zoals gezegd kunnen we via de omega de periode van de trilling bepalen. Een periode (T) betekent dat als we de periode bij een bepaald tijdstip optellen dat we terug opdezelfde positie moeten komen als bij het oorspronkelijke tijdstip
$$ y(t) = y(t + T) $$
Dus:
$$ A \cdot sin(\omega t + \phi) = A \cdot \sin(\omega (t + T) + \phi) $$
$$ \sin(\omega t + \phi) = \sin(\omega t + \omega T + \phi) $$
$$ \omega t + \phi + k \cdot 2 \pi = \omega t + \omega T + \phi $$
$$ 0 + k \cdot 2 \pi = \omega T $$
$$ \frac{2 \pi}{\omega} = T $$
ook:
$$ \frac{2 \pi}{T} = \omega $$
3.1.3 Snelheid, versnelling en energie
We kunnen vanuit de vergelijking van het vorige deel ook de snelheid en versnelling bepalen door ze gewoon af te leiden.
Eerste afgeleide is de snelheid, de tweede de versnelling.
Oorspronkelijke functie:
$$ y = A \cdot \sin(\omega t + \phi) $$
Eerste afgeleide:
$$ v_y = A \omega \cos(\omega t + \phi) $$
Dit is dus de snelheid op een gegeven tijdstip t.
$$ a_y = -A \omega^2 \sin(\omega t + \phi) $$
Bovenstaande kunnen we natuurlijk vereenvoudigen want:
$$ A \cdot \sin(\omega t + \phi) = y $$
Dus:
$$ a_y = -\omega^2 \cdot y $$
Nu we dit allemaal hebben kunnen we ook de energie bepaalden.
Kinetische energie
$$ E_k = \frac{m \cdot v^2}{2} $$
$$ E_k = \frac{m \cdot A^2 \omega^2 \cos^2(\omega t + \phi)}{2} $$
Omega konden we schrijven via de defintiie van pulsatie als:
$$ \omega = \sqrt{\frac{k}{m}} $$
Gekwadrateerd zoals in de opgave wordt de totale formule dan:
$$ E_k = \frac{k \cdot A^2 \cos(\omega t + \phi)}{2} $$ k zijnde de veerconstante
Potentiële energie
Bij een veer werkt de volgende kracht in:
$$ F = -k \cdot y \text{ (y is de uitrekking van de veert) } $$
Uit 2.2.3 weten we dat de de integraal moeten berekenen om de arbeid (potentiële energie) te vinden in een bepaalde interval van een variabele kracht.
(we zoeken de arbeid tussen y, de uitrekking en 0 de evenwichtstoestand van de veer) $$ E_p = W = \int_y^0 -k y dy $$
$$ E_p = -\frac{1}{2} [k \cdot y^2]_y^0 $$
$$ E_p = \left(-\frac{1}{2}\right) \cdot (k \cdot 0^2 - k \cdot (y)^2) $$
$$ E_p = \frac{1}{2} k y^2 $$
y is onze plaatsfunctie van hierboven.
$$ E_p = \frac{1}{2} \cdot A^2 \sin^2(\omega t + \phi) $$
3.2 Slingerbeweging
3.2.1 De slingerwetten
- Verband tussen slingerhoek en periode: er is geen verband tussen de hoekamplitude (slingerhoek) en de periode
- Verband tussen massa en periode: er is geen verband tussen de massa en de periode
- Verband tussen periode en de slingerlengte: er is een verband tussen de periode en de slingerlengte: hoe langer de slinger hoe langer de periode duurt
- Verband tussen de periode en g: de zwaarteveld sterkte is omgekeerd evenredig met de periode
Dit alles zorgt ervoor dat we kunnen komen tot de volgende vergelijking:
$$ T = 2 \pi \sqrt{\frac{l}{g}} $$
3.3 Golven
3.3.1 Lopende golven
3.3.1.1 Soorten golven
Indeling naargelang middenstof:
- Mechanische golven: golven die een middenstof nodig hebben om zich voort te planten
- Bv. golven in een veer, geluid (middenstof = lucht)…
- Elektromachnetische golven: golven die geen middenstof nodig hebben om zich voor te planten
Indeling naargelang beweging:
- Transversale golven = golven waarvan de trilrichting loodrecht staat op de voorplantingsrichting (vergelijkbaar met sinus golven)
- Lichtgolven zijn transversaal
- Longitudinale golven:
- Golven waarvan de voortplantingsrichting dezelfde is als de trilrichting (bv. Geluidsgolven)
3.3.1.2 Golflengte
De golflengte is de afstand tussen twee punten die in fase bewegen. Concreet betekent dit dat de twee punten op een bepaald tijdstip t op dezelfde hoogte zitten (y).
Vertrekkend vanaf deze defintie krijgen we voor de golflengte:
$$ \lambda = v \cdot T $$
Waarbij v de voortplantingssnelheid van de golf is.
3.3.1.3 Algemene uitdrukking van de golf
Soms willen we ook weten welke y een golf heeft in een bepaald tijdstip op een bepaalde plaats. Laten we beginnen te kijken hoe de positie van een golf eruit ziet in de oorsprong:
$$ y_0 = A \sin \omega t $$
met
$$ \omega = \frac{2 \pi}{T} $$
dus:
$$ y_0 = A \sin \frac{2 \pi t}{T} $$
Als we nu een ander punt gaan pakken in de plaats van de oorsprong dan gaat het tijdstip waarop dat punt beweegt anders zijn dan dat van de oorsprong. We weten dat de afstand dat een punt in een golf aflegt gelijk is aan de snelheid maal de tijd.
Als je auto 30km/u rijdt en je 2 uur rijdt dan heb je een afstand van 2*30 = 60 km gereden
$$ x = v \cdot t $$
Dus het tijdstip dat de het punt in x beweegt is:
$$ \frac{x}{v} = t' $$
Dan wordt onze eerste formule weer:
$$ y = A \frac{2\pi}{T} \sin(t - t’) = A \frac{2\pi}{T} \sin(t - \frac{x}{v}) $$
$$ y = A 2 \pi \sin\left(\frac{t}{T} - \frac{x}{v \cdot T}\right) $$
Aangezien:
$$ \lambda = v \cdot T $$
Dan:
$$ y = A 2 \pi \sin\left(\frac{t}{T} - \frac{x}{\lambda}\right) $$
Dat is dus onze formule van de uitwijking in x op een bepaald tijdstip t.
3.4 Geluid
3.4.1 Intensiteit van een toon
Ons oor neemt het geluid waar in een logaritmische schaal. Als men het reële geluidsniveau linear zou verhogen zou ons oor er niet meteen veel van horen. Pas als het veel luider staat kunnen we het opmerken.
In formules (N is het intensiteitsniveau):
$$ N = 10 \log \frac{I}{I_0} $$
N wordt uitgedrukt in dB of decibels.
De I_0 is de gehoorsdrempel, de drempel vanaf waar we effectief geluid kunnen horen.
$$ I_0 = 10^{-12} \frac{W}{m^2} $$
Vanaf 120 dB wordt de pijngrens overschreden dan krijgen we ook een pijnindruk en is de kans op gehoorsschade groot.